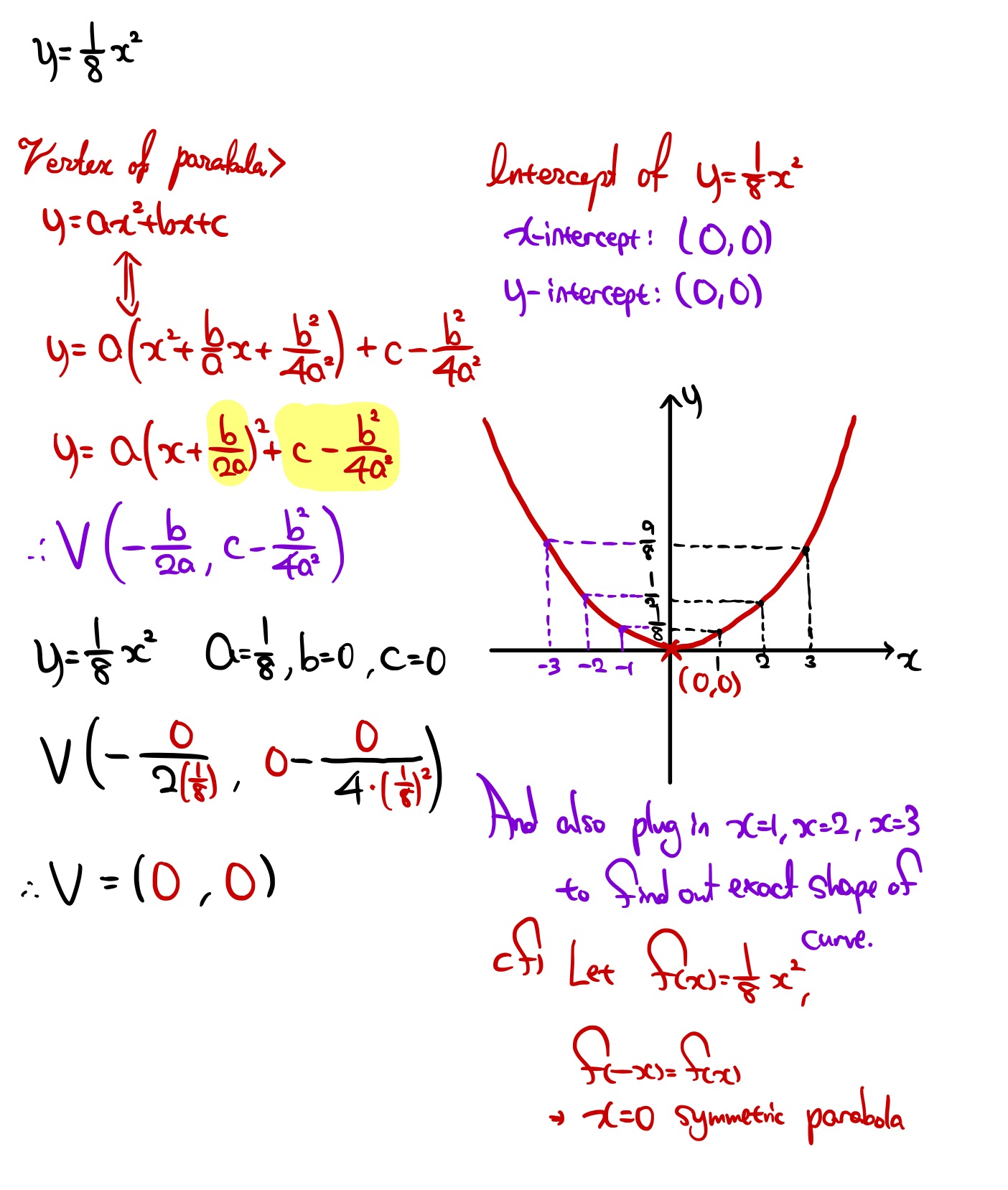
Y=x^2 3 parabola 137475-Y x 2 parabola
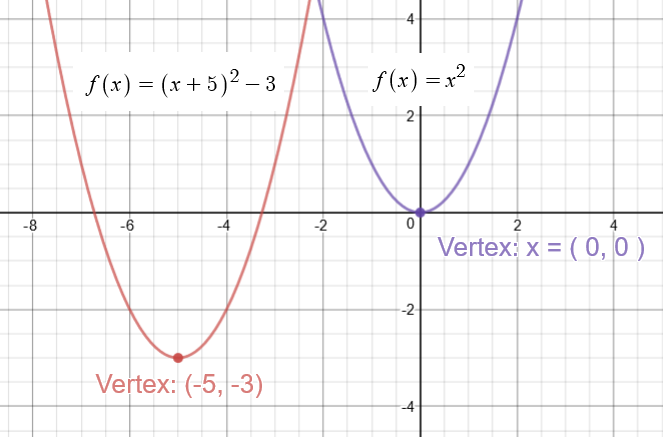
How To Graph A Parabola Y X 5 2 3 Socratic
So, the equation will be x 2 = 4ay Substituting (3, 4) in the above equation, (3) 2 = 4a(4) 9 = 16a a = 9/16 Hence, the equation of the parabola is x 2 = 4(9/16)y Or 4x 2 = 9y Go through the practice questions given below to get a thorough understanding of the different cases of parabolas explained above Practice Problems 1 Finding the yintercept of a parabola can be tricky Although the yintercept is hidden, it does exist Use the equation of the function to find the yintercept y = 12x 2 48x 49 The yintercept has two parts the xvalue and the yvalue Note that the xvalue is always zero So, plug in zero for x and solve for y y = 12(0) 2 48(0) 49 (Replace x with 0) y = 12 * 0 0 49
Y x 2 parabola
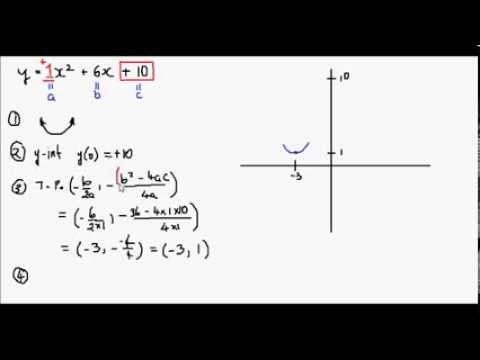
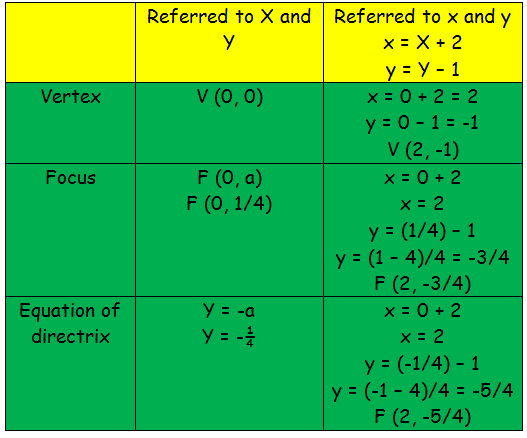
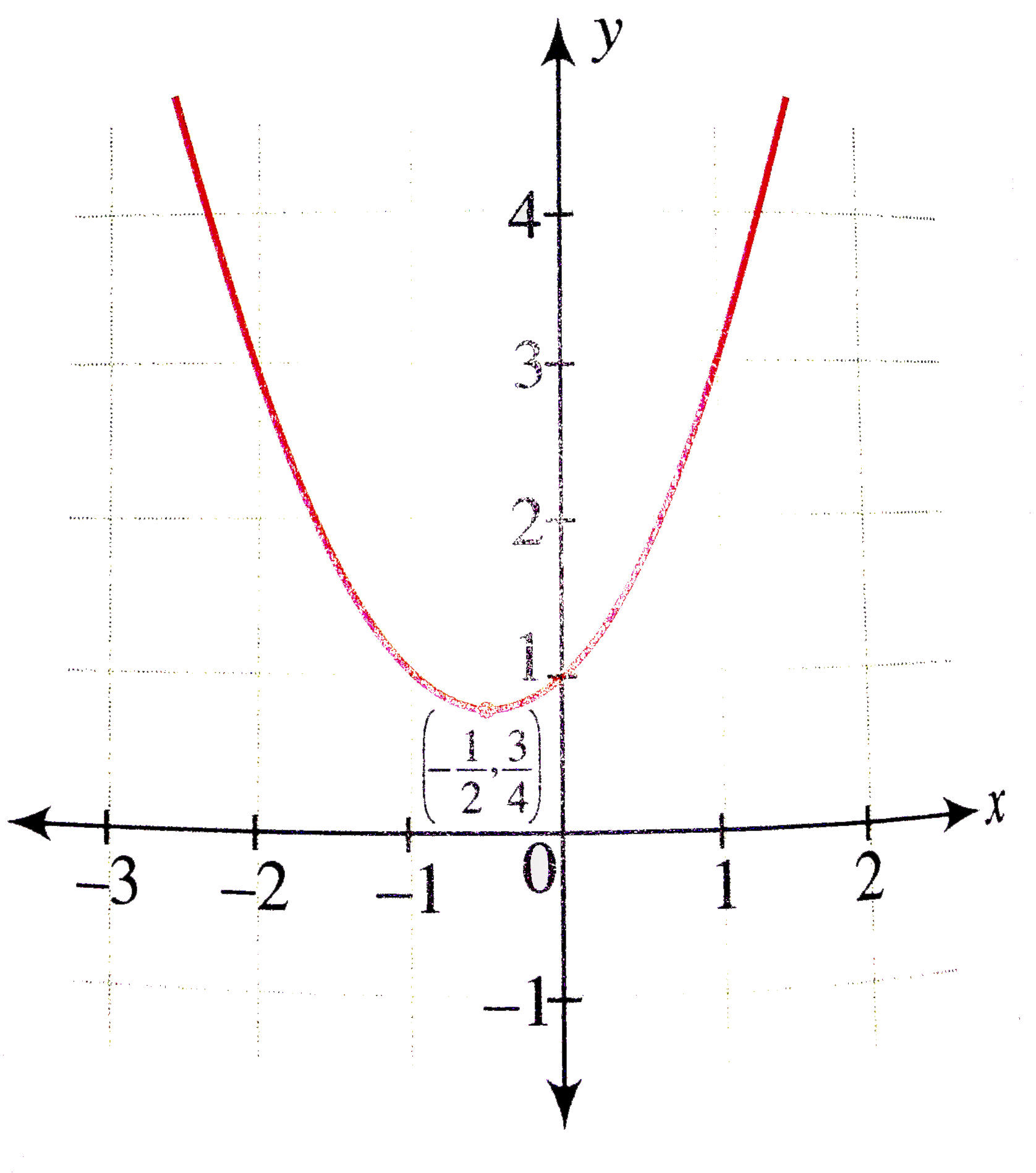
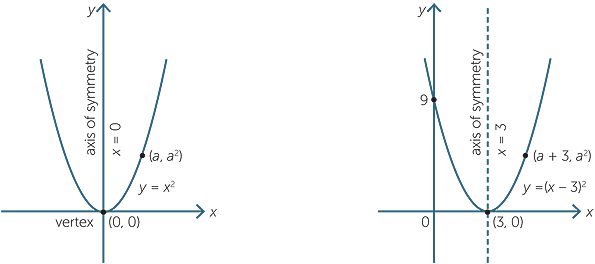
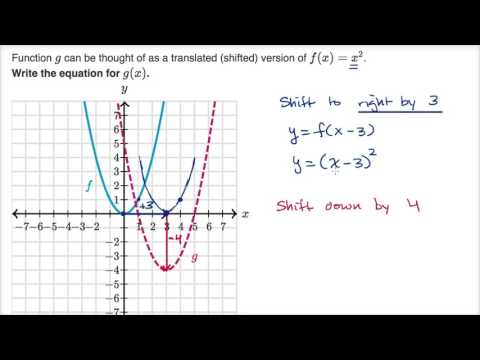
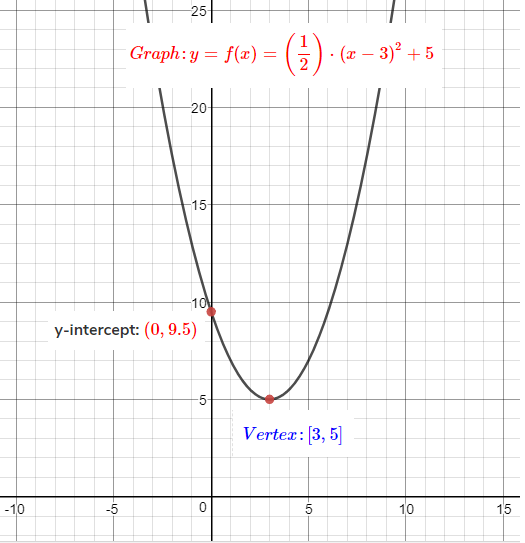
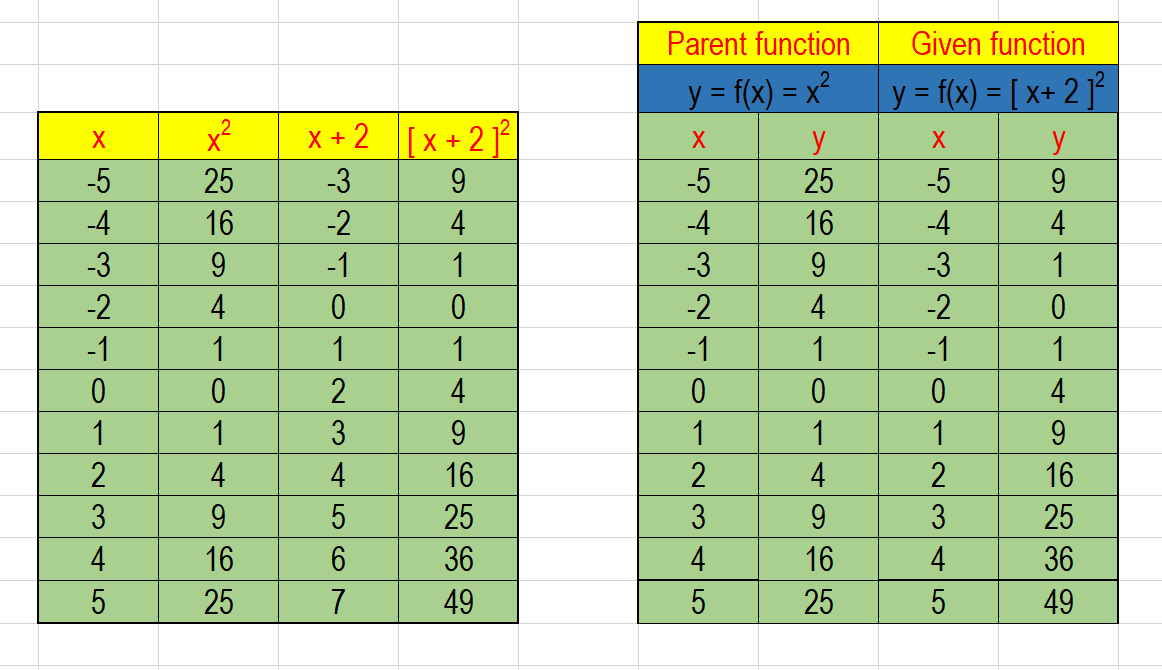
Y x 2 parabola-Y= (xh)^2 k with (h,k) being the vertex, this parabola has a vertex at (0, 1/4) If you are trying to factor it to find the xintercepts (aka the roots, the zeroes, or the solutions), this is also really easy, as the equation is a difference of perfect squares and can be factored into conjugates, lThe first form, which is usually referred to as the standard equation of a parabola is y = ax 2 bx c, where a, b, and c are constants and a is not equal to zero The focus of this paper is to determine the characteristics of parabolas in the form y = a(x h) 2 k For our purposes, we will call this second form the shiftform equation of a parabola
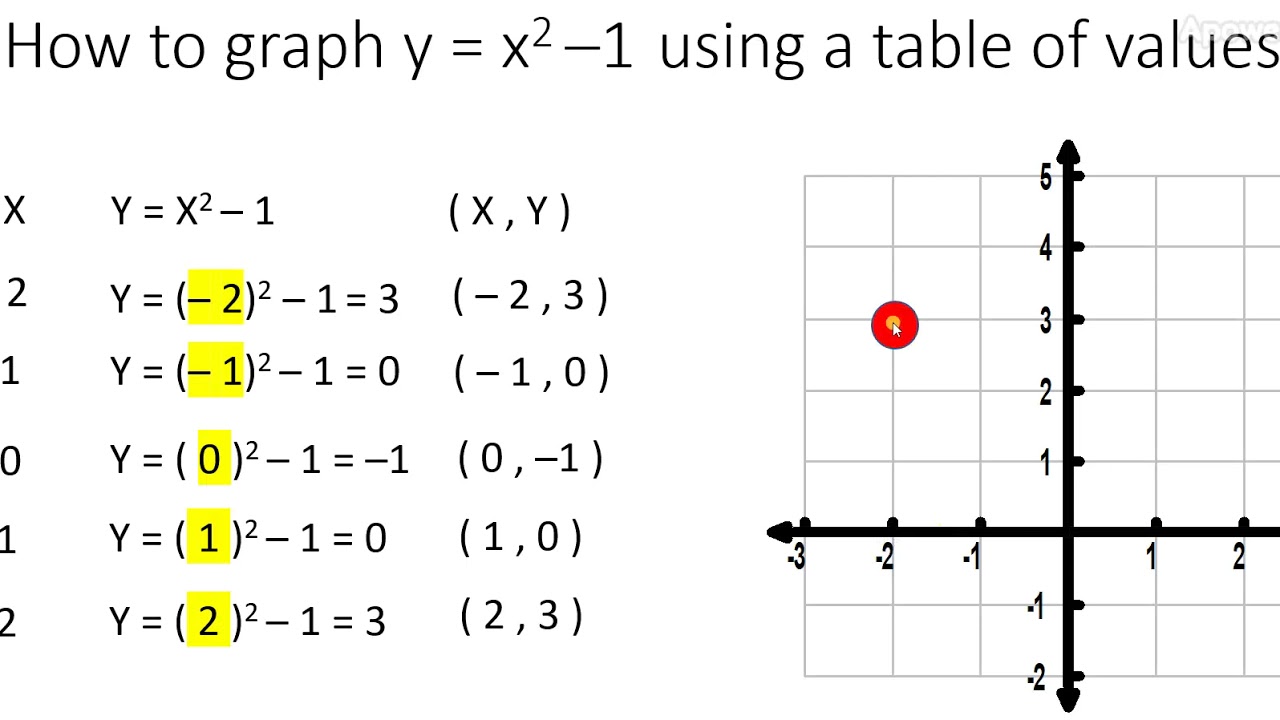
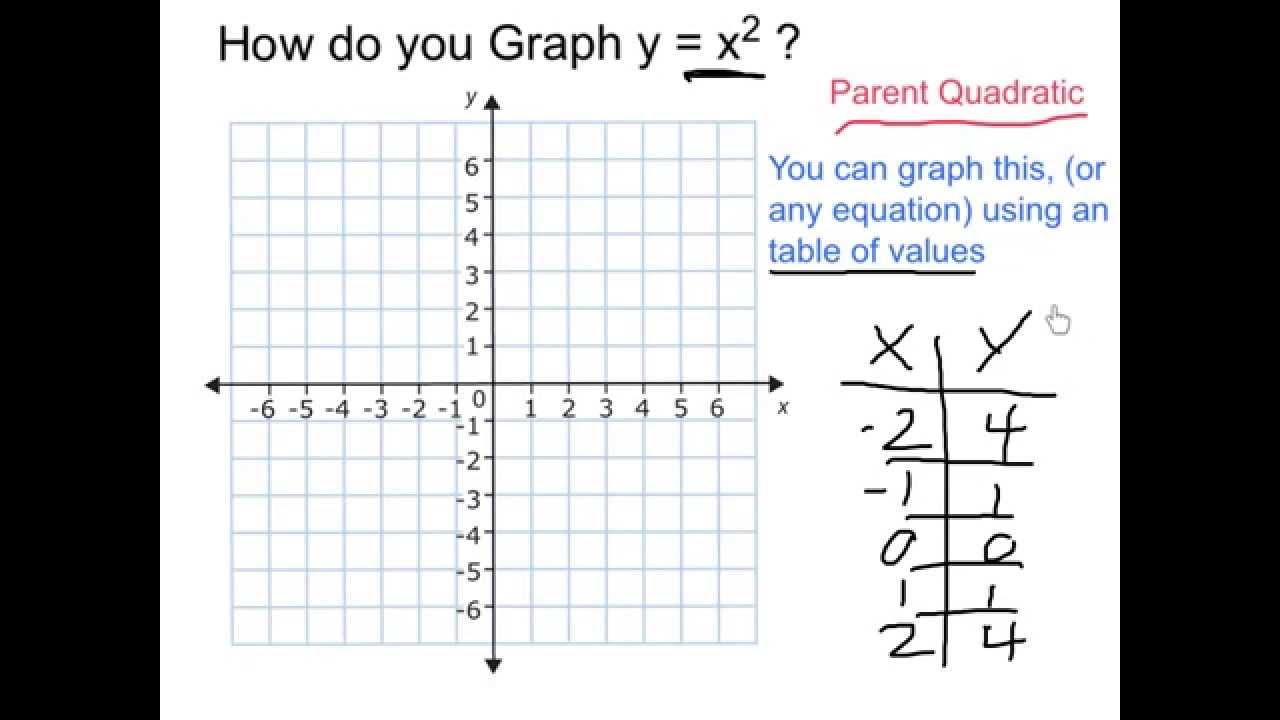
Graph Y X 2 1 Parabola Using A Table Of Values Video 3 Youtube
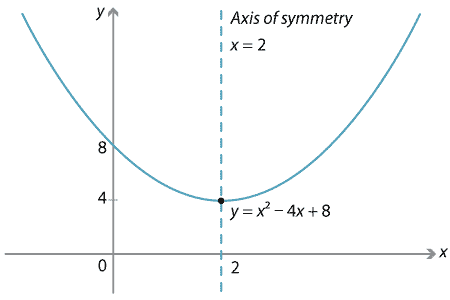
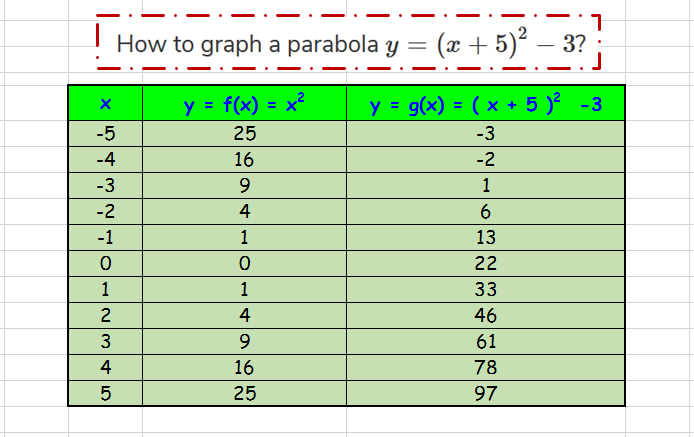
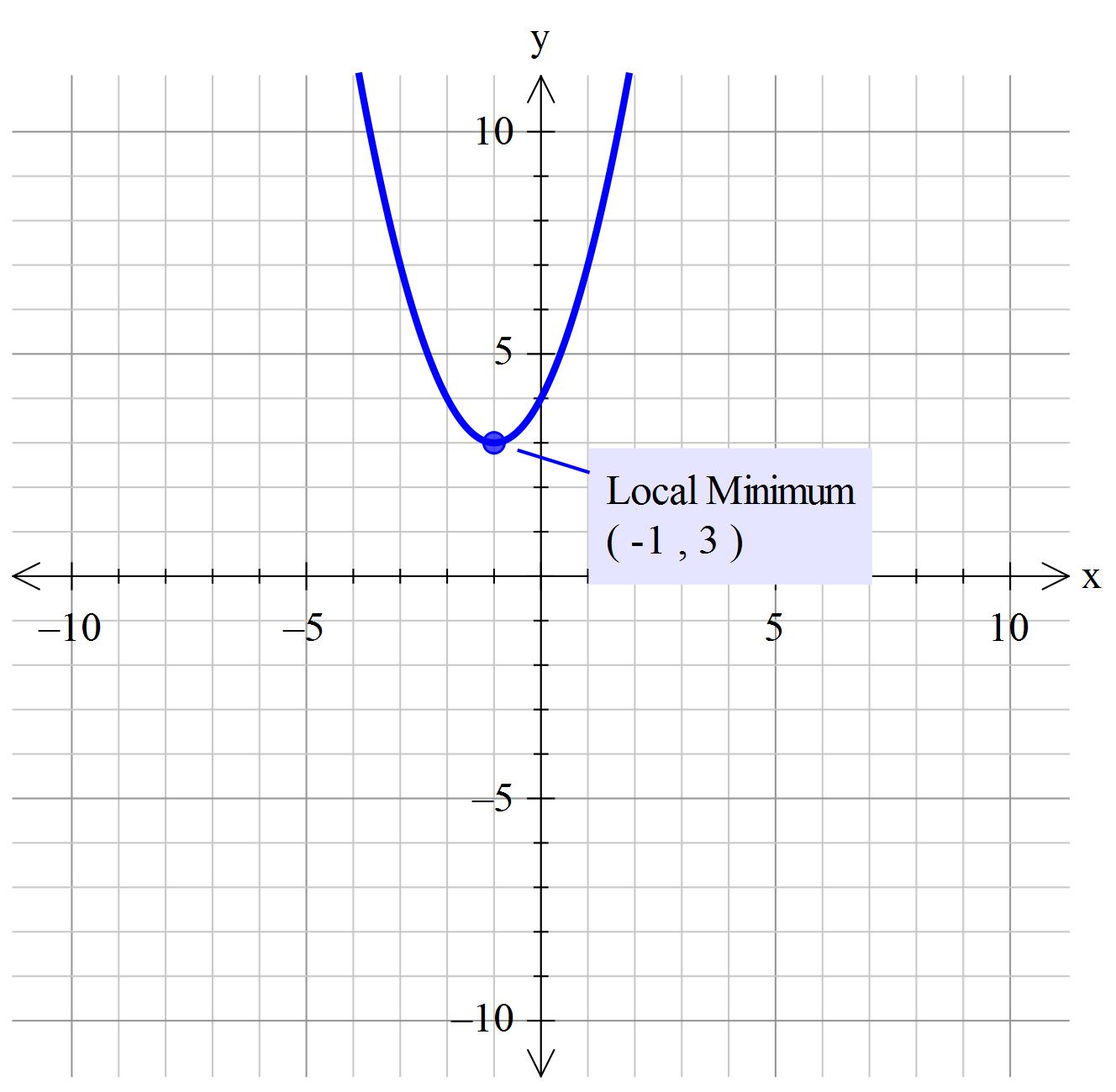
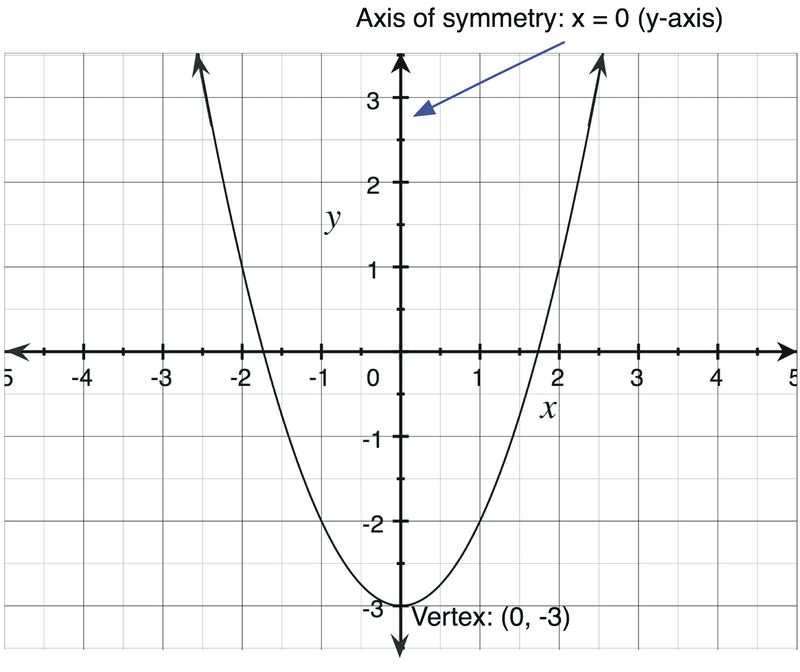
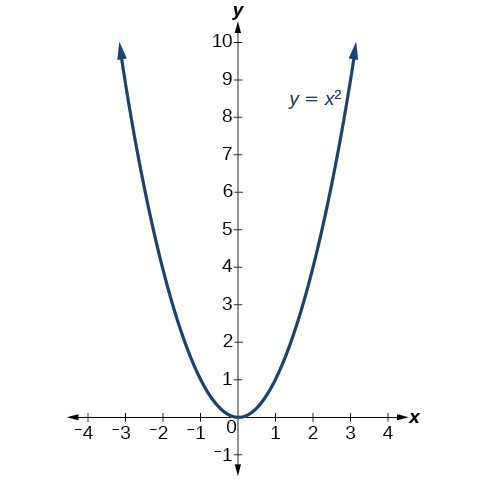
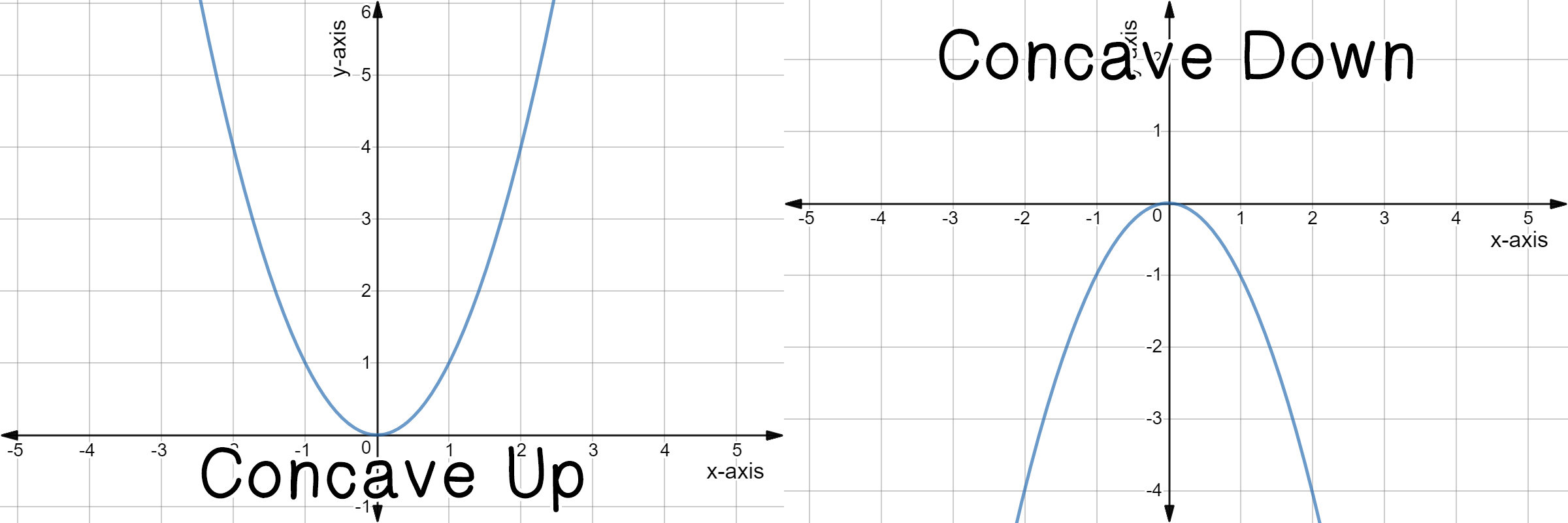
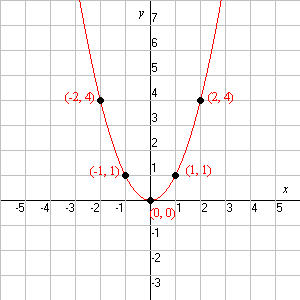
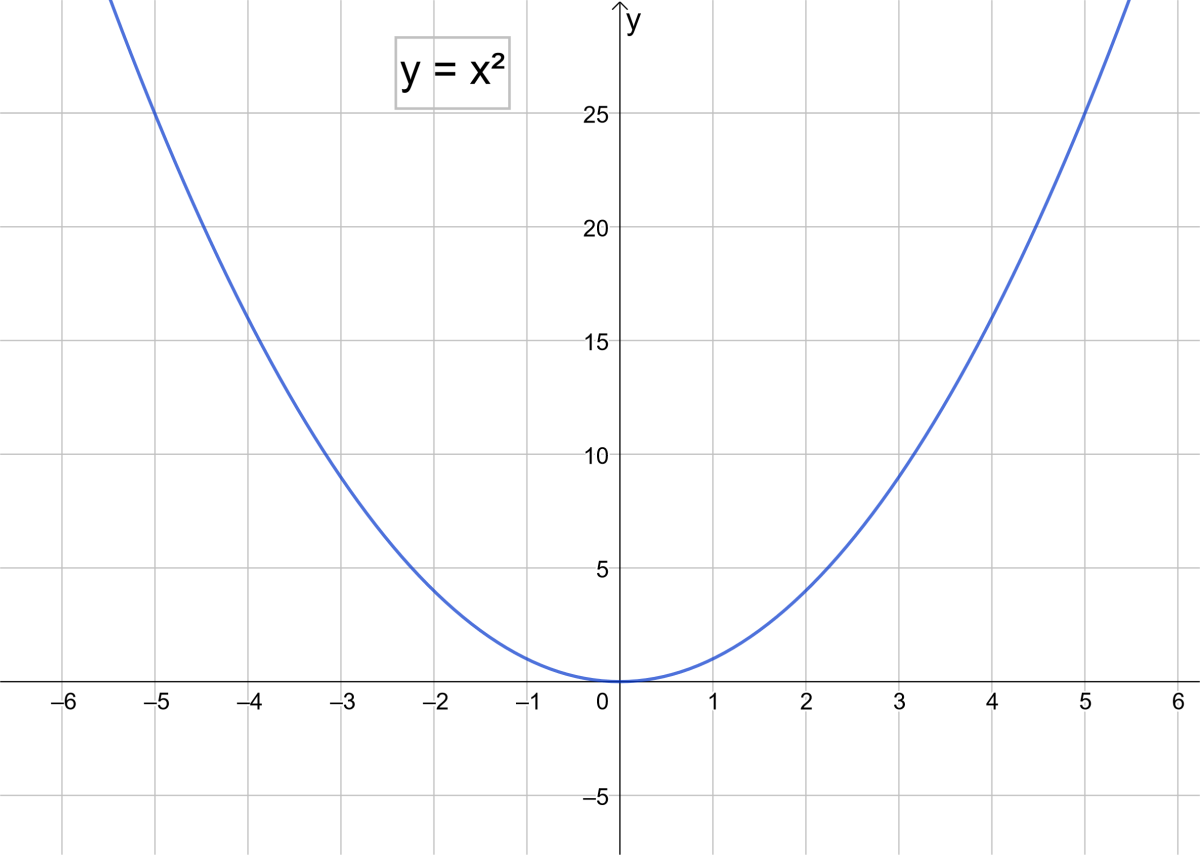
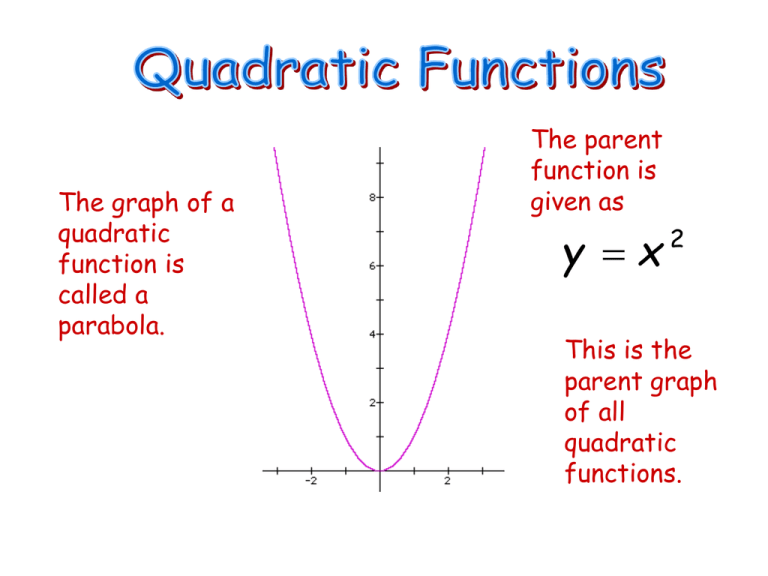
0 x a According to the arc length formula, L(a) = Z a 0 p 1 y0(x)2 dx = Z a 0 p 1 (2x)2 dx Replacing 2x by x, we may write L(a) = 1 2 Z 2a 0 p 1 x2 dx Thus theGraphing y = (x h)2 k In the graph of y = x2, the point (0, 0) is called the vertex The vertex is the minimum point in a parabola that opens upward In a parabola that opens downward, the vertex is the maximum point We can graph a parabola with aY = x 2 3x 13;
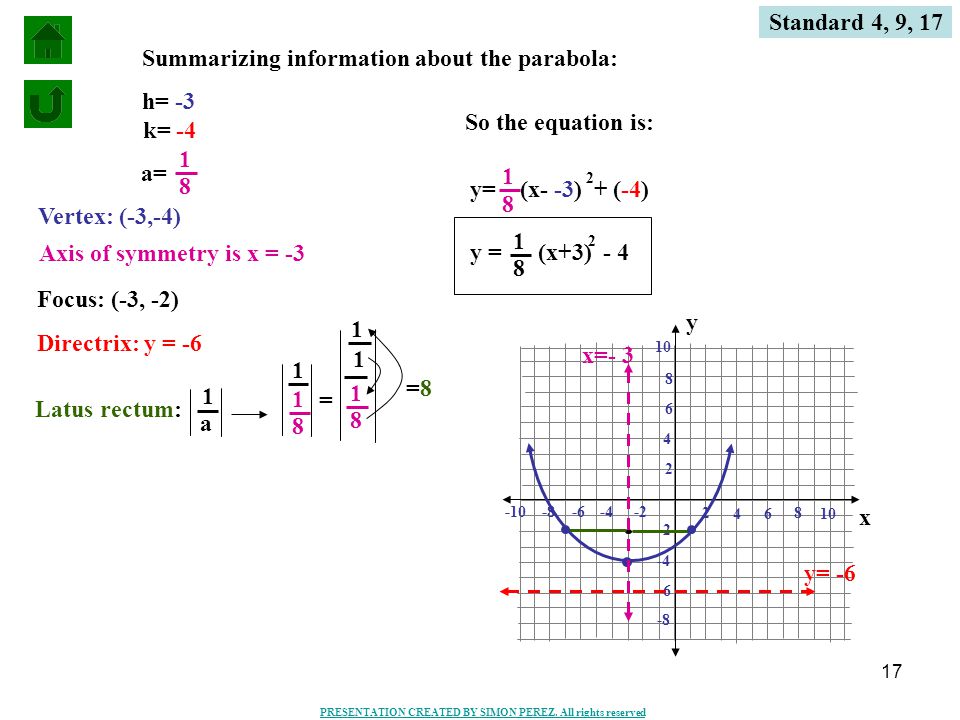
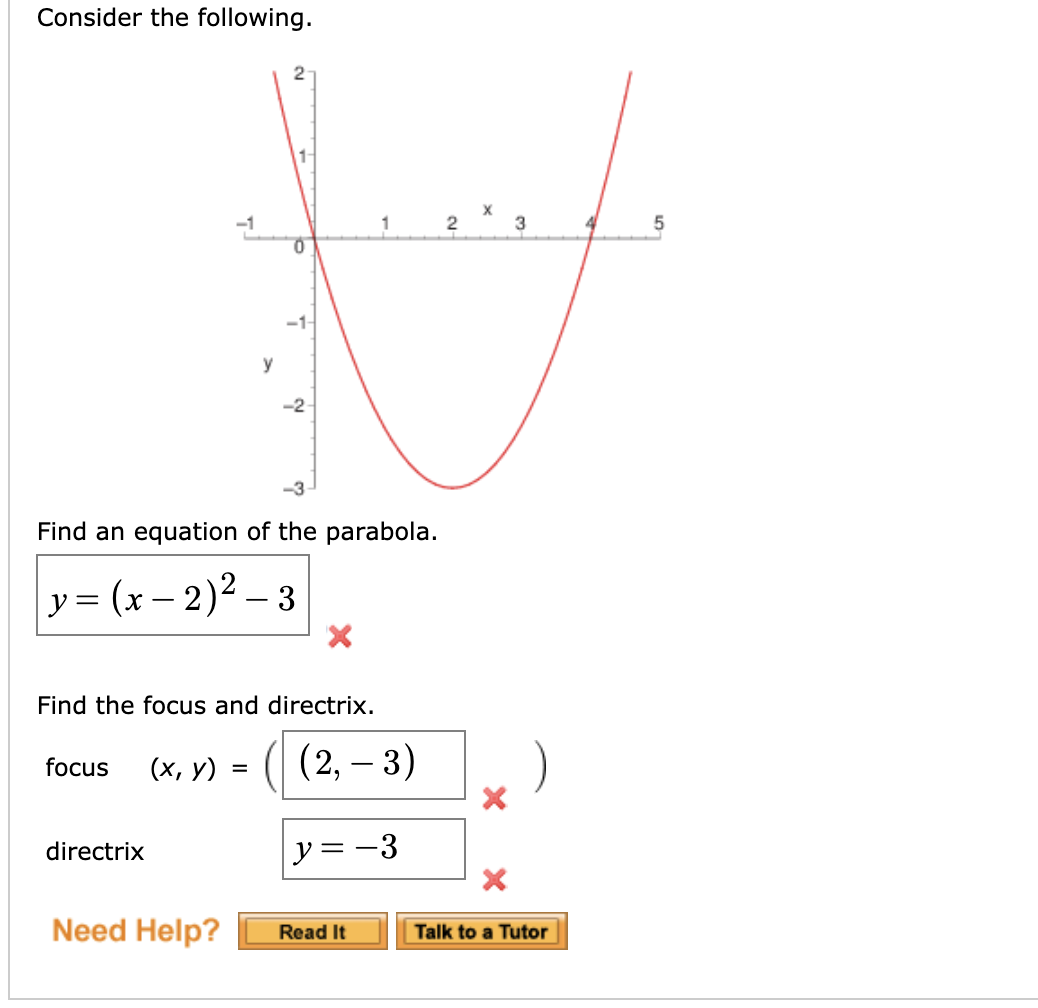
You're gonna get y is equal to 1/6, x minus one, squared, plus 1/2 There you go That is the parabola with a focus at (1,2) and a directrix at y equals 1 FascinatingSimilarly, if we are given an equation of the form y 2 AyBxC=0, we complete the square on the y terms and rewrite in the form (yk) 2 =4p(xh)From this, we should be able to recognize the coordinates of the vertex and the focus as well as the equation of the directrixWrite the equation of parabola in standard form y 2 8y = x 19 y 2 2(y)(4) 4 2 4 2 = x 19 (y 4) 2 4 2 = x 19 (y 4) 2 16 = x 19 Add 16 to each side (y 4) 2 = (x 3) (y 4) 2 = (x 3) is in the form of (y k) 2 = 4a(x h) So, the parabola opens up and symmetric about xaxis with vertex at (h, k) = (3, 4)
Y x 2 parabolaのギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 |  | |
 | ||
 |  | |
「Y x 2 parabola」の画像ギャラリー、詳細は各画像をクリックしてください。
 | ||
 |  |  |
 |  |  |
「Y x 2 parabola」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
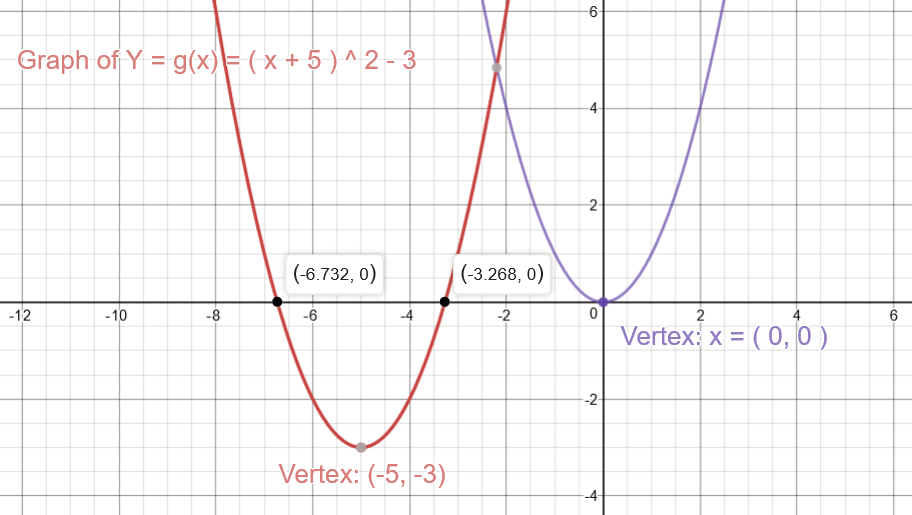 | ||
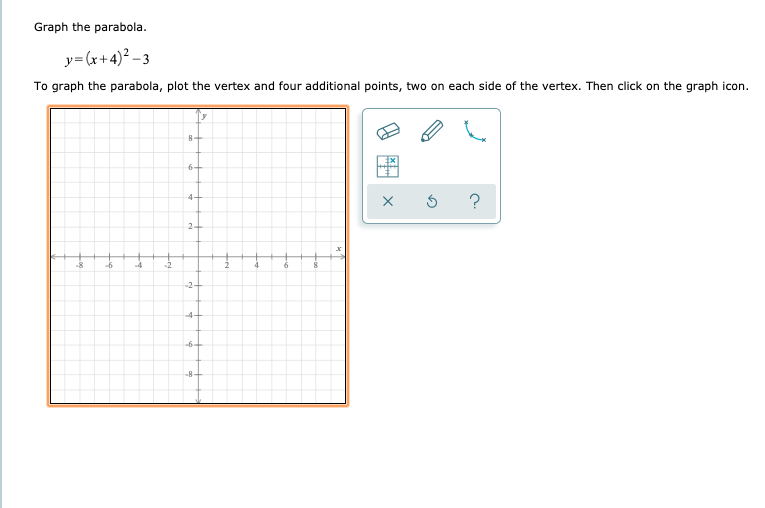 |  |  |
「Y x 2 parabola」の画像ギャラリー、詳細は各画像をクリックしてください。
 | 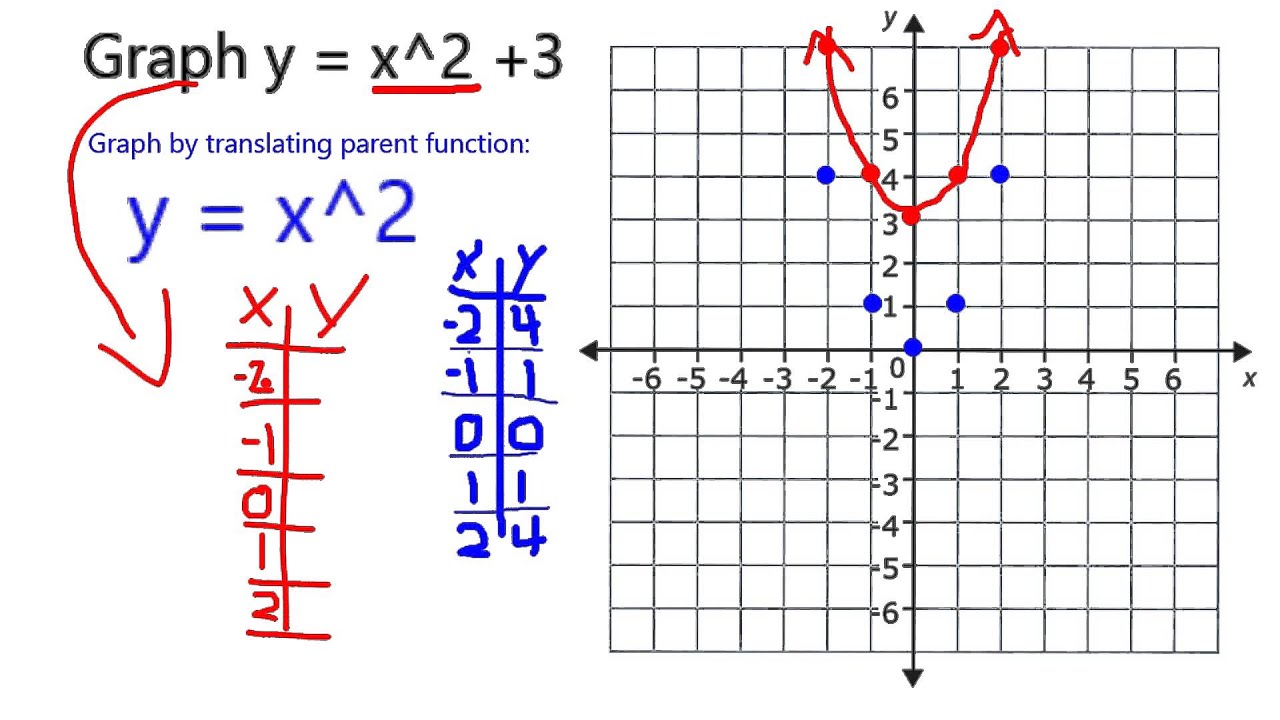 | 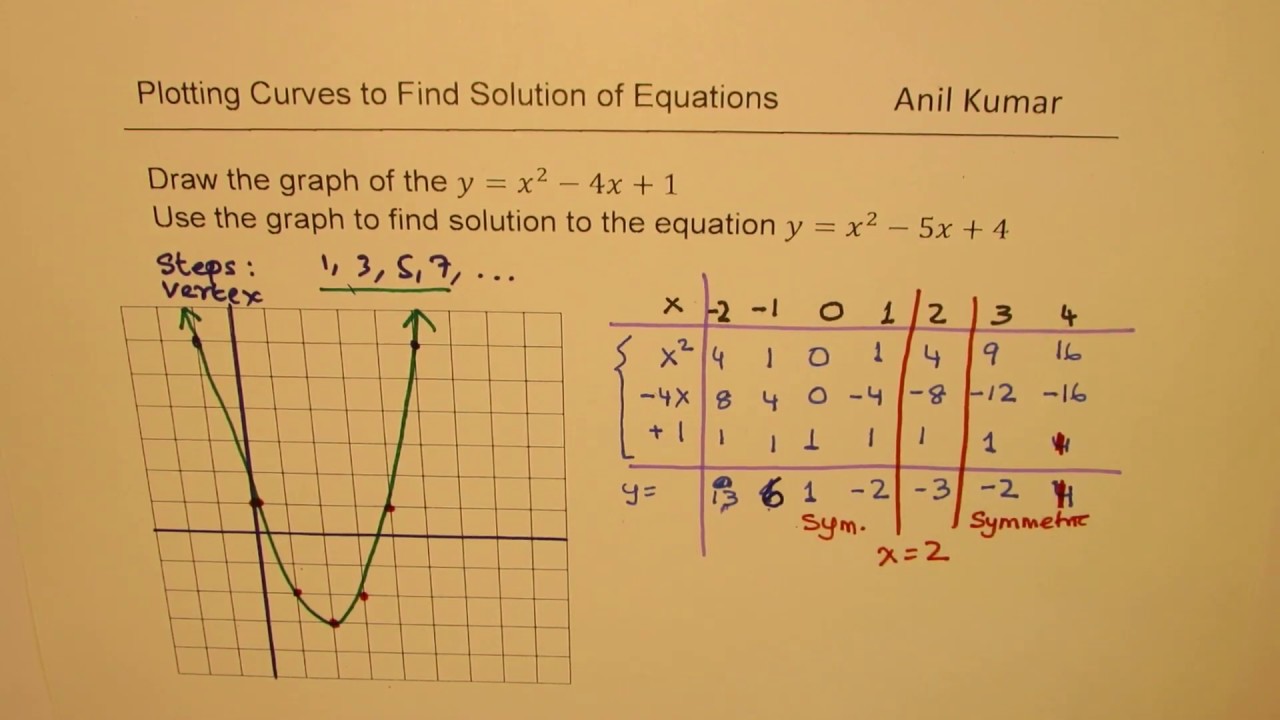 |
 |  |  |
 |  | |
「Y x 2 parabola」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 | ||
 |  |  |
「Y x 2 parabola」の画像ギャラリー、詳細は各画像をクリックしてください。
 | ||
 | ||
 |  |  |
「Y x 2 parabola」の画像ギャラリー、詳細は各画像をクリックしてください。
 | ||
 |  |  |
 |  | |
「Y x 2 parabola」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
「Y x 2 parabola」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  | |
「Y x 2 parabola」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  | |
「Y x 2 parabola」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 | ||
 | ||
「Y x 2 parabola」の画像ギャラリー、詳細は各画像をクリックしてください。
 | ||
 |
Axis\(y3)^2=8(x5) directrix\(x3)^2=(y1) precalculusparabolacalculator y=3\left(x3\right)^{2}2 en Related Symbolab blog posts Practice, practice, practice Math can be an intimidating subject Each new topic we learn has symbols and problems we have never seen The unknowingAnswer (1 of 3) The following is the equation of the parabola under consideration y ^ 2 4x 3 = 0 {\color{red}0} The standard form of a rightwards opening parabola is (y k) ^ 2 = 4p (x h) {\color{red}1} And the equation of the directrix of such a curve takes the form x = h
Incoming Term: y x 2 parabola, y x 2 parabolic cylinder,
コメント
コメントを投稿